Mathematical Notation for JavaScript Developers Explained

Being able to understand and implement mathematics in JavaScript can be very useful. This is particularly true when working with highly visual and interactive applications, something JavaScript is well suited to. However, it can be hard to make sense of it all and how it translates to code without a background in mathematics.

In this post, I'll explain some of the most common mathematical concepts and their symbols. I'll also provide examples so you can see how these concepts can be implemented in JavaScript. By the end of this post, you should have a better understanding of what those symbols mean and how you can translate them to code.

Dot and cross symbols

The dot and cross symbols are common in mathematics, but their uses differ depending on the context.

Scalar multiplication

Both symbols can represent the simple multiplication of scalars. The following are equivalent:

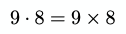
Generally, in JavaScript, the asterisk is used for multiplication:

const result = 9 * 8;

The multiplication sign is often only used to avoid ambiguity. For example, here it is omitted entirely:

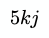
If the variables are scalars, the code will look like this;

const result = 5 * k * j;

Vector multiplication

For vector multiplication, often, an open dot ∘ is used. This symbol represents the Hadamard product.

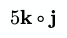
In JavaScript, it could be implemented like this:

function multiply(a, b) {
  return [a[0] * b[0], a[1] * b[1]];
}

function multiplyScalar(a, scalar) {
  return [a[0] * scalar, a[1] * scalar];
}

const s = 5;
const k = [1, 2];
const j = [2, 3];

const v = multiply(k, j);
const result = multiplyScalar(v, s);
// [ 10, 30 ]

Dot product

The dot symbol · can denote the dot product of two vectors. Sometimes this is called the scalar product as it evaluates to a scalar.

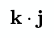
The code for this could look like this:

function dot(a, b) {
  return a[0] * b[0] + a[1] * b[1] + a[2] * b[2];
}

const k = [0, 1, 0];
const j = [1, 0, 0];

const result = dot(k, j);
// 0

The result of 0 means that the vectors are perpendicular.

Cross product

The cross symbol × can denote the cross product of two vectors.

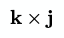
In code, it would look like this:

function cross(a, b) {
  const ax = a[0],
    ay = a[1],
    az = a[2],
    bx = b[0],
    by = b[1],
    bz = b[2];

  const rx = ay * bz - az * by;
  const ry = az * bx - ax * bz;
  const rz = ax * by - ay * bx;
  return [rx, ry, rz];
}

const k = [0, 1, 0];
const j = [1, 0, 0];

const result = cross(k, j);
// [ 0, 0, -1 ]

Sigma

The sigma symbol Σ is used for summation. Basically, summing up numbers.

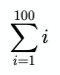
Here, i=1 means start at 1 and end at the number above the sigma, 100. These are the lower and upper bounds, respectively. The i to the right of the Σ tells us what we are summing. In code this can take the following form:

let sum = 0;
for (let i = 1; i <= 100; i++) {
  sum += i;
}
// 5050

Here is another slightly more complicated example:

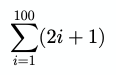
And the code for this:

let sum = 0;
for (let i = 1; i <= 100; i++) {
  sum += 2 * i + 1;
}
// 10200

Sigma can also be nested, with the right-most sigma getting evaluated first unless the expression uses parentheses to alter the order.

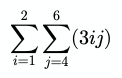
And in code:

let sum = 0;
for (let i = 1; i <= 2; i++) {
  for (let j = 4; j <= 6; j++) {
    sum += 3 * i * j;
  }
}
// 135

Capital Pi

The capital Pi or 'Big Pi' is very similar to sigma, except that it uses multiplication instead of summation to find the product of a sequence of values.

Here is an example:

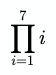
In code, it might look like this:

let value = 1;
for (let i = 1; i <= 7; i++) {
  value *= i;
}
// 5040

Bars

Bars are another one that can mean different things depending on the context. Below are three common uses: absolute value, Euclidean norm, and determinant. These all describe the length of an object.

Absolute value

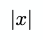
This means the absolute value of x. In JavaScript, it looks like this:

const x = -4;
const result = Math.abs(x);
// 4

Euclidean norm

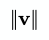
The Euclidean norm is concerned with vectors, and it's also known as the 'magnitude' or 'length' of a vector.

Here is an example using an array of [x, y, z] to represent a 3D vector:

function length(vector) {
  const x = vector[0];
  const y = vector[1];
  const z = vector[2];
  return Math.sqrt(x * x + y * y + z * z);
}

const result = length([0, 6, -8]);
// 10

Determinant

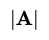
Here is an example of calculating the determinant of a 2x2 matrix, represented by a flat array.

function determinant(a) {
  return a[0] * a[3] - a[2] * a[1];
}

const result = determinant([1, 0, 0, 1]);
// 1

Hat

The 'hat' symbol is commonly used in geometry to represent a unit vector. For example, here is the unit vector of a:

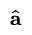
In Cartesian space, a unit vector typically has a length of 1. This means each part of the vector will be in the range of -1.0 to 1.0. The following example 'normalizes' a 3D vector into a unit vector:

function normalize(vector) {
  const x = vector[0];
  const y = vector[1];
  const z = vector[2];
  const squaredLength = x * x + y * y + z * z;

  if (squaredLength > 0) {
    const length = Math.sqrt(squaredLength);
    return [x / length, y / length, z / length];
  }
  return vector;
}

const result = normalize([0, 8, -6]);
// [ 0, 0.8, -0.6 ]

Element

In set theory, the 'element of' symbols ∈ and ∋ are often used to describe whether something is an element of a set. For example:

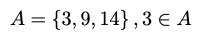
Here there is a set of numbers A { 3, 9, 14 }, and it is saying 3 is an 'element of' that set.

A simple implementation might look like this:

const A = [3, 9, 14];

const result = A.indexOf(3) >= 0;
// true

The backwards ∋ is the same, but the order changes:

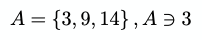
You can also use the 'not an element of' symbols ∉ and ∌ like so:

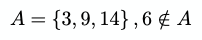
Functions

Functions are a core part of mathematics, and they translate to code quite naturally.

A function is a way of describing what happens to an input variable in order to get the output result. For example, the following is a function:

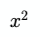
This function can be given a name typically ƒ would be used, but it could be A(x) or anything else.

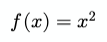
In code, you might give it a more meaningful name, like square and write it like this:

function square(x) {
  return Math.pow(x, 2);
}

Functions can also have multiple parameters. These are known as arguments in mathematics, and the number of arguments a function takes is known as the arity of the function.

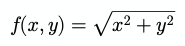
In code:

function length(x, y) {
  return Math.sqrt(x * x + y * y);
}

Piecewise function

Functions can be thought of as having three main parts: the input, the relationship, and the output. The relationship being how the input relates to the output. Some functions will use different relationships depending on the input value. The following function ƒ chooses between two 'sub functions' depending on the input value.

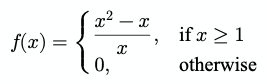
This is very similar to if / else in code.

function f(x) {
  if (x >= 1) {
    return (Math.pow(x, 2) - x) / x;
  }
  return 0;
}

Common functions

Some functions are widespread in mathematics. For a developer, these are similar to built-in functions, like parseInt in JavaScript.

One example is the sgn function. This is the signum or sign function. Using piecewise function notation, it looks like this:

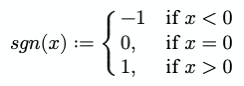
In code, it might look like this:

function sgn(x) {
  if (x < 0) return -1;
  if (x > 0) return 1;
  return 0;
}

Floor & ceiling

The special brackets ⌊x⌋ and ⌈x⌉ represent the floor and ceil functions, respectively.

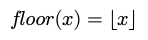
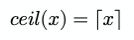
In code:

Math.floor(x);
Math.ceil(x);

When the two symbols are mixed ⌊x⌉, it typically represents a function that rounds to the nearest integer:

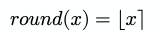
In code:

Math.round(x);

Final thoughts

This is a big topic to explore, and this article just scratches the surface. If you'd like to find out more, a good starting point is the math-as-code repository which was an inspiration for this article.

A handy way to run the above code examples is via the RunJS app. RunJS is a JavaScript playground available for Mac, Windows and Linux. It runs your code and gives you live feedback as well as a number of other powerful features. Give it a try.